Formal Verification (National Institute of Advanced Industrial Science and Technology)



Research Staff
-

Professor
Reynald AFFELDT -

Associate Professor
Yusuke KAWAMOTO
Research Areas
Formal verification methods are mathematically rigorous techniques for checking the correct behavior of software and hardware systems. Various techniques and tools for formal verification have been applied to developing, e.g., bug-free programs, secure cryptographic protocols, and reliable operating systems. Nowadays, formal verification appears essential to build a trusted and secure digital society. In our laboratory, we study formal methods for specifying and verifying software systems with uncertainties that deal with, e.g., physical environments, probability, and statistics. This includes the application of formal verification methods to guarantee the safety of cyber-physical systems such as robots, to prevent security vulnerabilities of software, and to rigorously verify and explain statistical programs and artificial intelligence systems. For that purpose, we conduct research on the formalization of mathematics, programming languages, and related topics of theoretical computer science.
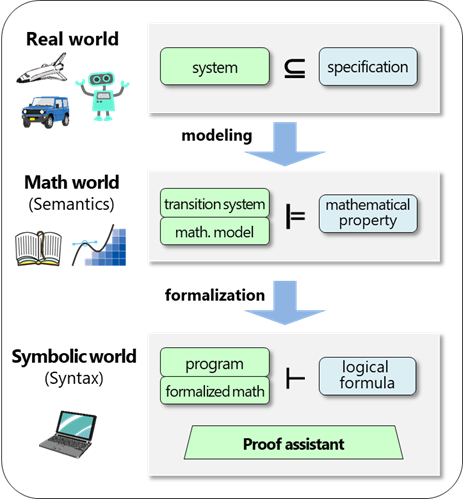
Formal verification and proof assistants
Our primary tool to perform formal verification is proof assistants. A proof assistant is a piece of software that checks mathematical proofs written in formal logic. This checking mechanism is based on research on formal logic and type theory.
Using a proof assistant, one develops reusable libraries of formal definitions and theorems to represent formally computer programs, systems, and mathematics in general. We are mostly using the Coq proof assistant.
Software safety
Security vulnerabilities of software are our primary concern.
Problems arise because of
- the complexity of modern software (e.g., using machine learning as a component)
- uncertainties due to interaction with the physical environment (e.g., cyber-physical systems, robots) or due to large input data sets (e.g., in AI)
Current research:
- formalization of probabilistic programs (sample paper: CPP 2023, APLAS 2023)
- formalization of programs with effects probabilities (sample paper: J Funct Program 2021)
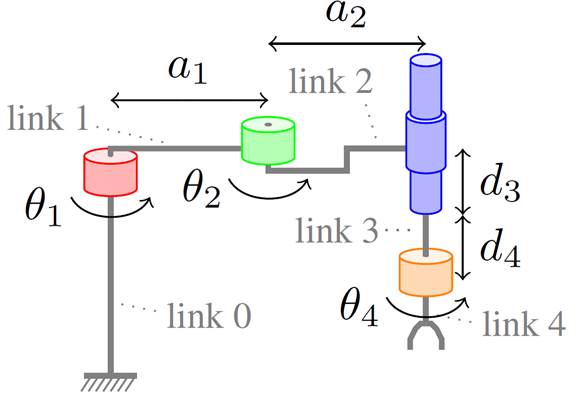
- formalization of robotics in Coq (sample paper: CPP 2017)
- Formal methods for statistical program (sample paper: Artif. Intell. 2024)
Formalization of mathematics
The rigorous verification of software relies largely on mathematical theories: statistical programs and artificial intelligence systems using probability theory and statistics, algebraic methods to verify robots and functional programs, real analysis to study the physics of cyber-physical systems.
Current research:
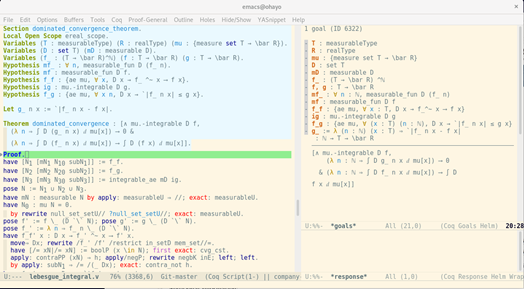
- Formal verification of Analysis (sample paper: J Autom Reason 2023)
- Formal verification of Information theory (sample paper: J Autom Reason 2020)
Key Features
About AIST
AIST (National Institute of Advanced Industrial Science and Technology) is one of the largest public research organizations in Japan. We are affiliated with the Digital Architecture Research Center which is in the Tokyo Bay area.
Basic knowledge to start research
- A strong interest in applications of mathematics to software verification.
- Basic knowledge in formal logic and in the semantics of programming languages (functional programming languages, type theory, etc.).
Guidance policy
- We expect students to acquire basic knowledge of formal verification techniques and will then discuss research topics according to the students' interests.
- We are ready to discuss spontaneous research proposals from students and provide guidance, in English, Japanese, or French.
- We expect initiatives from the student and an appropriate commitment to research discussions and progress monitoring.
- We will mainly conduct research meetings online, but we expect students to come to the AIST Waterfront (Koto-ku, Tokyo) on a regular (or long-term) basis.
What students could learn
Our goal is to guide students to develop
- the knowledge and practice of software verification and formal mathematics
- logical and abstract reasoning skills useful to design software systems
- technical writing skills (in English or in Japanese) developed through the practice of research surveys and scientific presentations